discomop.blogg.se - The simple linear regression equation

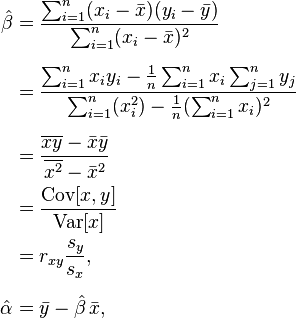
This function provides simple linear regression and Pearson's correlation. Menu location: Analysis_Regression and Correlation_Simple Linear and Correlation. Open topic with navigation Simple Linear Regression and Correlation Let us say you are the professor and you want to use this prediction equation to estimate what two of your students might get on their final exam.Simple Linear Regression and Pearson Correlation - StatsDirect One unit increase in the score of Exam1 would increase the final score by 1.85. In this example, Y = 15.6 + 1.85 × X, where X is the score on Exam 1 and Y is the final exam score. The estimates of slope and intercept are shown in “Parameter Estimate” section. The R square value says that 89.5% of the variability can be explained by this model. The p-value is 0.0001 therefore, we reject the null and claim the model is statistically significant. The p-value of the F-test is lower than the α level (0.05), indicating that the model is statistically significant. “Analysis of Variance” section provides an ANOVA table covering degrees of freedom, sum of squares, and mean square information for total, regression and error. 89.5% of the variability in the data can be accounted for by this linear regression model. R 2 measures the percentage of variation in the data set that can be explained by the model. If not significant, we will need to re-examine the predictor or look for new predictors before continuing. Step 4: Check whether the model is statistically significant.

The regression analysis results appear in the new window.

Check the box of “Residuals” so that the residuals can be saved automatically in the last column of the data table.

Select “FINAL” as “Response” and “EXAM1” as “Continuous Predictors.”.

A new window named “Regression” pops up.

Click Stat → Regression → Regression → Fit Regression Model.

Step 3: Run the simple linear regression analysis. It appears you could “fit” a line through these data points. The higher the score on exam one, the higher the score on the final.

A scatter plot is generated in a new window.īased on the scatter plot, the relationship between exam one and final seems linear.

Select “FINAL” as “Y variables” and “EXAM1” as “X variables.”.

A new window named “Scatterplot– Simple” pops up.

A new window named “Scatterplots” pops up.

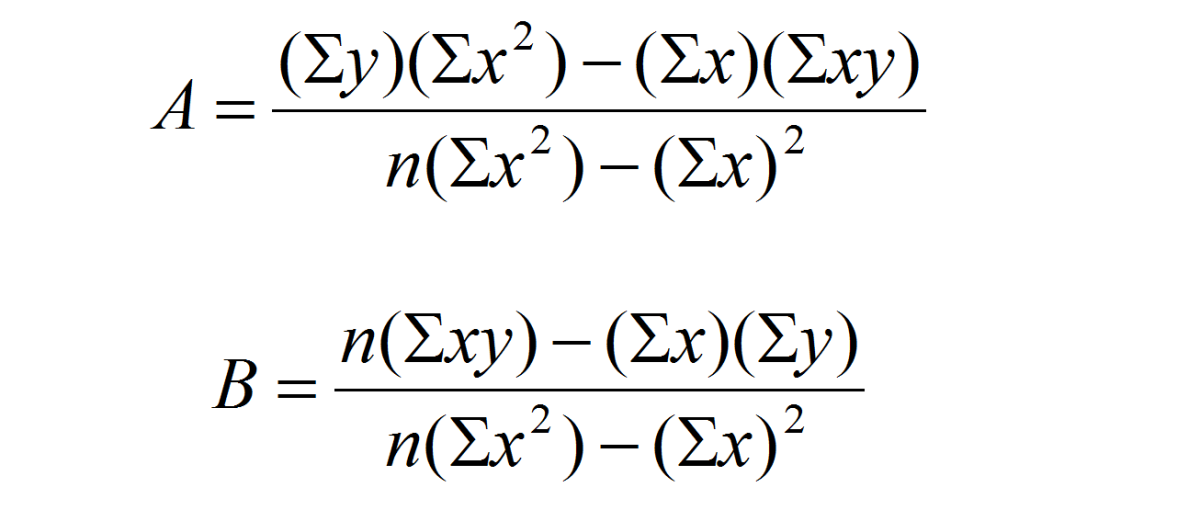
Step 2: Create a scatter plot to visualize whether there seems to be a linear relationship between X and Y. X (independent variable) is the score of exam one.Y (dependent variable) is the score of final exam.

The fitted value of the dependent variable:īy using calculus, it can be shown the sum of squared error is minimal when The actual value of the dependent variable: In mathematical language, we look for α and β that satisfy the following criteria: the vertical difference between the data point and the fitting line). It estimates the unknown parameters of the regression equation by minimizing the sum of squared residuals (i.e. The ordinary least squares is a statistical method used in linear regression analysis to find the best fitting line for the data points. It is the difference between the actual Y and the fitted Y (i.e. β is the intercept indicating the Y value when X is equal to 0 α is the slope describing the steepness of the fitting line.Y is the dependent variable (the response) and X is the single independent variable (the predictor).